Кривые Безье являются основой векторной графики, и основным ее элементом, на основе которого строятся все более сложные изображения. Кривые Безье строятся по двум точкам, соединенным между собой отрезком, а кривизна этого отрезка задается а зависимости от длины и угла наклона пары векторов, являющихся касательными к этому отрезку. В случае, если векторы, корректирующие кривизну отрезка, отсутствуют, или принадлежат ему, то отрезок соединяет две соседние точки по кратчайшему расстоянию между ними.
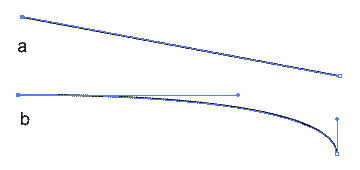
Рис. 1. Пример кривых Безье.
На рисунке изображение "a" показывает пример кривых Безье, в которых отсутствуют изменяющие кривизну соединительного отрезка векторы. На рисунке "b" синим цветом показаны такие векторы, и результирующая кривизна соединяющего точки отрезка.
Кривые Безье названы в честь французского инженера Пьера Безье, который одним из первых математически описал эти векторные формы, применяемые ныне в векторной и инженерной графике.